% A Haskell Compiler
% David Terei
% (GHC Developer)
# A Haskell Compiler
* How does a Haskell compiler work?
* Can all reason about how a C compiler works but Haskell seems
difficult
* Will try to give you an idea of how GHC works
# Structure of Lecture
Will first give an overview of the intuitive ideas behind the
compiler.
Then will go through how GHC works in terms of traditional compiler
stages:
* _Front End: Haskell -> Core_
Lexer, Parser, Renamer, Typecheck, Desugar
* _Middle: Core -> Core_
Optimisation passes
* _Backend: Core -> Assembly_
STG Machine, Code Generator, RTS, Backends (C, LLVM, NCG)
# Why is Haskell difficult
Haskell is seen as a difficult language to understand from a
compilation perspective.
There are some good reasons for this:
* Higher order functions
* Lazy evaluation
* Partial application
* Syntax that hides allocation
* Typechecker
But one reason (an annoying one) is the use of Jargon
# Terminology 101
Two good resources for dealing with unknown terminology:
* [Foldoc: Free online dictionary of computing](http://foldoc.org/)
* [The Memory Management Refernce](http://www.memorymanagement.org/)
Lets cover some of the terminology now:
* _Values_: Both data and functions
* _Unboxed_: Primitive (machine level) types, not "boxed up" on the
heap
* _Closure_: Heap allocated data associated with a method
* _Thunk_: A suspended computation
* _Continuations_: The cousin of closures. Unlike a closure you aren't
simply calling a function, you are continuing a saved execution
state. Basically though, if you have closures and tail calls as
Haskell does, continuations can be built.
Yes, closures, thunks and continuations are all very similar. One
implementation can capture them all, however the terminology is used
to capture the different use cases.
# Statistics of GHC
* GHC is written in Haskell
* Compiler: 227,000 lines of Haskell (including comments)
* Libraries: 242,000 lines of Haskell (including comments)
* The run-time system is written in C
* 87,000 lines of C
* Started in 1989
* 23 developers contributed current release (7.4, in development since
Aug 6th) with over 500 commits
# Pipeline of GHC
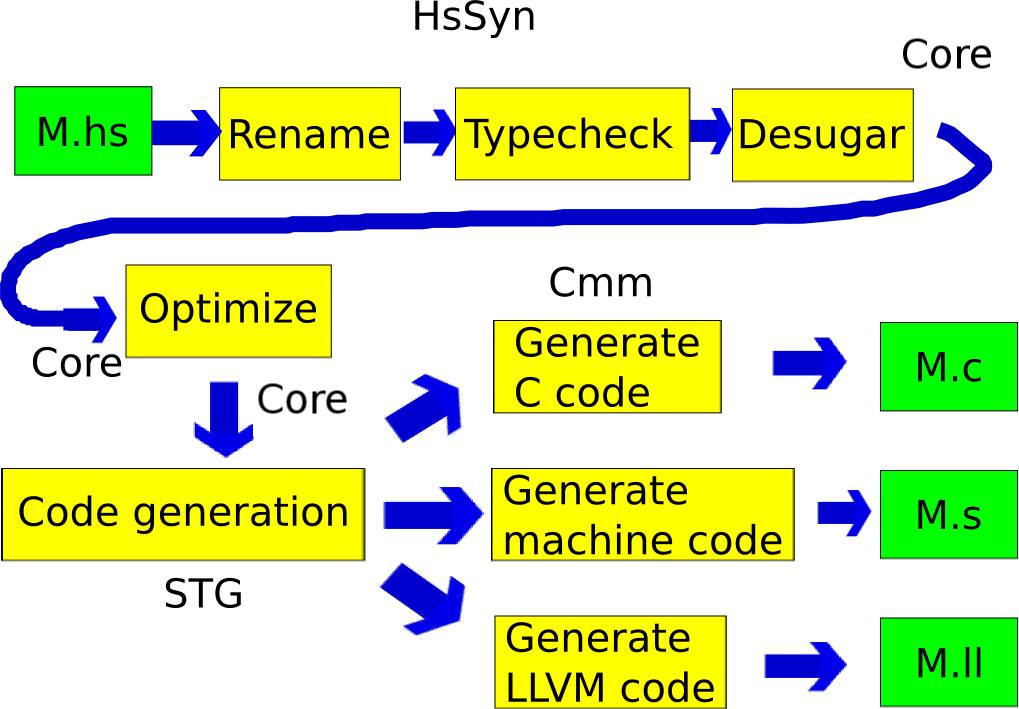
# Core
We will start though with a quick look at Core, the main intermediate
language used by GHC:
* Functional lazy language
* It consists of only a hand full of constructs!
~~~
variables, literals, let, case, lambda abstraction, application
~~~
* In general think, `let` means allocation, `case` means evaluation
* For the curious, Core is technically a variant of a `System FC`
(which is itself a variant of `System F`)
* Basic idea of Core (and the various System \ which are
extensions of simple typed lambda calculus) is to be the smallest
language needed to capture the source language. Easier to study,
reason, optimize...
Useful tool for viewing Core:
~~~~
cabal install ghc-core
~~~~
# Core in one slide
~~~~ {.haskell}
data Expr b -- "b" for the type of binders,
= Var Id
| Lit Literal
| App (Expr b) (Arg b)
| Lam b (Expr b)
| Let (Bind b) (Expr b)
| Case (Expr b) b Type [Alt b]
| Type Type
| Cast (Expr b) Coercion
| Coercion Coercion
| Tick (Tickish Id) (Expr b)
data Bind b = NonRec b (Expr b)
| Rec [(b, (Expr b))]
type Arg b = Expr b
type Alt b = (AltCon, [b], Expr b)
data AltCon = DataAlt DataCon | LitAlt Literal | DEFAULT
~~~~
# Graph Reduction
The way that lazy functional languages like Haskell are implemented is
through a technique called _graph reduction_
Its best to use the graph reduction model as an intuitive way to think
about how Haskell is evaluated, the actual way GHC implements Haskell
is pretty close to how an imperative language works.
~~~~ {.haskell}
f g = let x = 2 + 2
in (g x, x)
~~~~
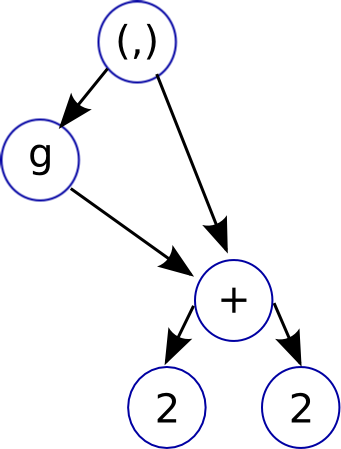
* Graph reduction allows lazy evaluation and sharing
* _let_: adds new node to graph
* _case_: expression evaluation, causes the graph to be reduced
* when a node is reduced, it is replaced (or _updated_) with its
result
# Terminology 102
* _redex(es)_:
reducible expression. A expression that can be evaluated further
* _normal form_:
an expression without an redexes
* _head normal form_:
an expression where the top level (head) is neither a redex NOR
a lambda abstraction with a reducible body
* _weak head normal form_:
an expression where the top level (head) isn't a redex
* _unfolding_:
unfolding of a function f is just the body of f.
* Unfolding = Inlining.
# Terminology 103
* evaluation strategies:
* _call-by-value_: arguments evaluated before function entered
(copied)
* _call-by-name_: arguments passed unevaluated
* _call-by-need_: arguments passed unevaluated but an expression
is only evaluated once (sharing)
* _no-strict evaluation_ Vs. _lazy evaluation_:
* non-strict: Includes both call-by-name and call-by-need, general
term for evaluation strategies that don't evaluate arguments
before entering a function
* lazy evaluation: Specific type of non-strict evaluation. Uses
call-by-need (for sharing).
# Front End: _Haskell -> Core_
Lets now look at how Haskell is compiled to
[Core](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Compiler/CoreSynType).
* Core is a small lazy language functional language
* Learning Core is the most useful thing to get out of this lecture,
experienced Haskell programmers that care about performance will
look at Core.
* Think of it as a functional assembly language. Reasoning about
behaviour and performance of Core is much simpler
# Terminology 104
* _kernel_: A kernel in programming language domain means the
essential subset of the language. The 'base' of the language on
which all other constructs are defined.
* Core is a kernel for Haskell.
* _CAF_: (Constant Applicative Form) A top level constant, allocated
for life time of program and shared. Since statically allocated
garbage collector has to [treat them specially](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Rts/Storage/GC/CAFs?redirectedfrom=Commentary/Rts/Storage/CAFs)
* _scrutinee_: The expression you are case'ing on in a case statement
# Functions -> Core
Haskell
~~~~ {.haskell}
idChar :: Char -> Char
idChar c = c
id :: a -> a
id x = x
idChar2 :: Char -> Char
idChar2 = id
~~~~
Core
~~~~ {.haskell}
idChar :: GHC.Types.Char -> GHC.Types.Char
[GblId, Arity=1, Caf=NoCafRefs]
idChar = \ (c :: GHC.Types.Char) -> c
id :: forall a. a -> a
id = \ (@ a) (x :: a) -> x
idChar2 :: GHC.Types.Char -> GHC.Types.Char
idChar2 = id @ GHC.Types.Char
~~~~
* [GblId...] specifies various metadata about the function
* Functions are all lambda abstractions
* Explicit passing and instantiation of type variables
* type variables are proceeded by @ symbol (read them as 'at type
...')
* they are passed abstracted and passed around just like value
variables
* this is known as second order lambda calculus
* GHC uses this representation because it makes preserving type
information during optimization easy
# Functions -> Core
Haskell
~~~~ {.haskell}
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
~~~~
Core
~~~~ {.haskell}
map :: forall a b. (a -> b) -> [a] -> [b]
map =
\ (@ a) (@ b) (f :: a -> b) (xs :: [a]) ->
case xs of _ {
[] -> GHC.Types.[] @ b;
: y ys -> GHC.Types.: @ b (f y) (map @ a @ b f ys)
}
~~~~
* case statements are only place evaluation happens, read them as
'evaluate'
* they take an extra variable just after `of` that captures the
return value of the scrutinee
* names are fully qualified
# Data -> Core
Haskell
~~~~ {.haskell}
data Maybe a = Nothing | Just a
none = Nothing
some = Just (1 :: Int)
~~~~
Core
~~~~ {.haskell}
none :: forall a. Maybe a
none = Nothing
n :: GHC.Types.Int
n = GHC.Types.I# 1
some :: Maybe GHC.Types.Int
some = Just @ GHC.Types.Int n
~~~~
* Data types don't explicitly appear in Core
* Core supports datatype but just no syntax for them at this level
* Can see how GHC lifts constants out to the top level (CAFs)
* Can also see boxing and primitive types
* In general Core follows same syntactic rules as Haskell (e.g
Uppercase = Data constructor, # = unboxed value / type)
# Handling where
Haskell
~~~~ {.haskell}
dox :: Int -> Int
dox n = x * x
where x = (n + 2) * 4
~~~~
Core
~~~~ {.haskell}
dox :: GHC.Types.Int -> GHC.Types.Int
dox =
\ (n :: GHC.Types.Int) ->
let {
x :: GHC.Types.Int
x =
GHC.Num.* @ GHC.Types.Int GHC.Num.$fNumInt
(GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt n (GHC.Types.I# 2))
(GHC.Types.I# 4) }
in GHC.Num.* @ GHC.Types.Int GHC.Num.$fNumInt x x
~~~~
* `where` becomes `let`
# Patterns & Guards
Haskell
~~~~ {.haskell}
iff :: Bool -> a -> a -> a
iff True x _ = x
iff False _ y = y
~~~~
Core
~~~~ {.haskell}
iff :: forall a. GHC.Bool.Bool -> a -> a -> a
iff =
\ (@ a) (d :: GHC.Bool.Bool) (x :: a) (y :: a) ->
case d of _
GHC.Bool.False -> y
GHC.Bool.True -> x
~~~~
* Patterns and guards become `case` statements
# Sharing & Updating
Haskell
~~~~ {.haskell}
sum100 :: Int -> Int
sum100 n = foldr (+) 0 [1..100]
~~~~
Core
~~~~ {.haskell}
-- Unoptimized
sum100n = \ (n :: Int) -> * n (foldr (I# 0) (enumFromTo (I# 1) (I# 100)))
-- Optimized
sum100n = \ (n :: Int) -> GHC.Base.timesInt n sum100n1
sum100n1 = case $wgo 1 of r { __DEFAULT -> GHC.Types.I# r }
$wgo :: Int# -> Int#
$wgo = \ (w :: Int#) ->
case w of w'
__DEFAULT -> case $wgo (GHC.Prim.+# w' 1) of r
__DEFAULT -> GHC.Prim.+# w' r
100 -> 100
~~~~
* For the optimized case GHC lifts the constant expression out so its
only computed once and then shared
* Optimized version creates a new function called `$wgo` which means
'worker'. This version works with unboxed types for efficiency.
# Partial Evaluation -> Core
Haskell
~~~~ {.haskell}
add :: Int -> Int -> Int
add x y = x + y
add2 :: Int -> Int
add2 = add 2
~~~~
Core (unoptimized)
~~~~ {.haskell}
add :: GHC.Types.Int -> GHC.Types.Int -> GHC.Types.Int
add =
\ (x :: GHC.Types.Int) (y :: GHC.Types.Int) ->
GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt x y
x :: GHC.Types.Int
x = GHC.Types.I# 2
add2 :: GHC.Types.Int -> GHC.Types.Int
add2 =
\ (y :: GHC.Types.Int) ->
GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt x y
~~~~
* (+) function used is the polymorphic `GHC.Num.+` variant
* `GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumtInt` means, select the
(+) field from the GHC.Types.Int dictionary (which is retrieved
from GHC.Num.$fNumInt) for the GHC.Num type class
# Partial Evaluation -> Core
Haskell
~~~~ {.haskell}
add :: Int -> Int -> Int
add x y = x + y
add2 :: Int -> Int
add2 = add 2
~~~~
Core (optimized)
~~~~ {.haskell}
add :: GHC.Types.Int -> GHC.Types.Int -> GHC.Types.Int
Hs2Core.add = GHC.Base.plusInt
x :: GHC.Types.Int
x = GHC.Types.I# 2
add2 :: GHC.Types.Int -> GHC.Types.Int
add2 = GHC.Base.plusInt x
~~~~
* type class dictionary method has been inlined.
# (+) -> Core
The function `GHC.Base.plusInt` is implemented as:
~~~~ {.haskell}
+ :: Int -> Int -> Int
+ = \ a b -> case a of _
I# a_ -> case b of _
I# b_ -> I# (GHC.Prim.+# a_ b_)
~~~~
* Notice the evaluation and unboxing of each argument, followed
finally by reboxing.
# Type Classes -> Core
Haskell
~~~~ {.haskell}
typeclass MyEnum a where
toId :: a -> Int
fromId :: Int -> a
instance MyEnum Int where
toId = id
fromId = id
instance (MyEnum a) => MyEnum (Maybe a) where
toId (Nothing) = 0
toId (Just n) = 1 + toId n
fromId 0 = Nothing
fromId n = Just (fromId $ n - 1)
~~~~
Core
~~~~ {.haskell}
toId :: forall a. MyEnum a => a -> GHC.Types.Int
toId =
\ (@ a) (d :: MyEnum a) ->
case d of _ { D:MyEnum f1 _ -> f1 }
fromId :: forall a. MyEnum a => GHC.Types.Int -> a
fromId =
\ (@ a) (d :: MyEnum a) ->
case d of _ { D:MyEnum _ f2 -> f2 }
~~~~
# Type Classes -> Core
Core
~~~~ {.haskell}
$fMyEnumInt :: MyEnum GHC.Types.Int
$fMyEnumInt = D:MyEnum @ GHC.Types.Int (id @ GHC.Types.Int) (id @ GHC.Types.Int)
$fMyEnumMaybe :: forall a. MyEnum a => MyEnum (Maybe a)
$fMyEnumMaybe =
\ (@ a) ($dMyEnum_arR :: MyEnum a) ->
D:MyEnum @ (Maybe a_acF)
($fMyEnumMaybe_$ctoId @ a $dMyEnum_arR)
($fMyEnumMaybe_$cfromId @ a $dMyEnum_arR)
$fMyEnumMaybe_$ctoId :: forall a. Hs2Core.MyEnum a => Hs2Core.Maybe a -> GHC.Types.Int
$fMyEnumMaybe_$ctoId =
\ (@ a) ($dMyEnum_arR :: MyEnum a) (ds :: Maybe a) ->
case ds of _
Nothing -> GHC.Types.I# 0
Just n -> case toId @ a $dMyEnum_arR n of _
GHC.Types.I# y -> GHC.Types.I# (GHC.Prim.+# 1 y)
~~~~
* Typeclasses are implemented via _dictionaries_
* Just a data structure storing the various functions for each field
* Functions that have type class constraints take an extra dictionary argument
* GHC will optimize away this dictionary passing when it can
# IO -> Core
* Monads are just type classes. So much of previous applies.
* IO Monad is basically a state passing monad. Passes around the 'Real
World' so that IO actions can transform it.
~~~~ {.haskell}
newtype IO a = IO (State# RealWorld -> (# State# RealWorld, a #))
~~~~
* 'Real Wold' is represented in GHC by a special token
* At the base, there are some primitive IO actions.
* IO Monad builds on top of RealWord# and the primitive IO actions.
Haskell
~~~~ {.haskell}
f :: IO ()
f = do
putStrLn "Hello World"
putStrLn "What's up today?"
~~~~
# IO -> Core
Core (Unoptimized)
~~~~ {.haskell}
g :: GHC.Types.IO ()
g =
GHC.Base.>> @ GHC.Types.IO GHC.Base.$fMonadIO @ () @ ()
(System.IO.putStrLn (GHC.Base.unpackCString# "Hello World"))
(System.IO.putStrLn (GHC.Base.unpackCString# "What's up today?"))
~~~~
Core (optimized)
~~~~ {.haskell}
f :: GHC.Prim.State# GHC.Prim.RealWorld -> (# GHC.Prim.State# GHC.Prim.RealWorld, () #)
f =
\ (world :: GHC.Prim.State# GHC.Prim.RealWorld) ->
case hPutStr2 stdout f1 True world of _
(# new_world, _ #) -> hPutStr2 stdout f2 True new_world
f1 :: [GHC.Types.Char]
f2 = GHC.Base.unpackCString# "Hello World"
f2 :: [GHC.Types.Char]
f1 = GHC.Base.unpackCString# "What's up today?"
~~~~
* `unpackCString#` takes a C style string and turns it into a Haskell
String
# Lazy Evaluation -> Core
Haskell
~~~~ {.haskell}
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl' :: (a -> b -> a) -> a -> [b] -> a
forcee :: a -> b -> b
forccee = seq
~~~~
Core
~~~~ {.haskell}
foldl = \ (f :: a -> b -> a) (z :: a) (d :: [b]) ->
case d of _
[] -> z;
: x xs -> foldl f (f z x) xs
foldl' = \ (f :: a -> b -> a) (z :: a) (d :: [b]) ->
case d of _
[] -> z;
: x xs ->
case f z x of z'
__DEFAULT -> foldl' b f z' xs
forccee = \ (x :: a) (y :: b) -> case x of _ { __DEFAULT -> y }
~~~~
* Notice the exta `case` statement in foldl' to force evaluation
# Core Summary
* Look at Core to get an idea of how your code will perform
* Lots of noise in Core, so best to clean up manually (or play with
various flags to suppress some of the noise)
* Some rules:
* Pattern matching and guards are translated to case statements
* `where` statements become `let` statements
* language still lazy but looking for `let` and `case` gives you a
good idea of evaluation order
* `case` means evaluation. (e.g `seq` is translated to `case`)
* `let` statements are allocation of closures
* function application is a thunk
* operations involving unboxed types are eager
# Middle of GHC: _Core -> Core_
Hopefully you have a decent idea of how Haskell is reduced to Core
now. Once we have the Core IR we can do a lot of optimization work:
* Inlining, CSE, DCE
* Strictness
* Float In
* Full Laziness
* Specialise
* Spec Constr
* Liberate Case
* Lambda Eta Expansion
* Do Eta Reduction
* Case Merge
* Static Argument Transformation
# Some standard optimisations
* GHC does some stock standard optimisations: Inlining, Common
Subexpression Elimination, Dead Code Elimination
* A large set of simple, local optimisations (e.g constant folding)
are done in one pass called the _simplifier_. It is run repeatedly
until not further changes can be done (with a fixed maximum number
of iterations).
* These are only the basic, big win ones. All the other standard stuff
(e.g strength reduction, loop induction...) are missing.
* We get a lot of this for free though if we use the LLVM backend.
Rest of the optimisations GHC does are fairly specific to a functional
language. Lets look at a few of them.
~~~~
Fun Fact: Estimated that functional languages gain 20 - 40%
improvement from inlining Vs. imperative languages which gain 10 - 15%
~~~~
# STG Code
* In the next few slides the code Ill be showing isn't exactly Core
but a IR GHC uses after Core called STG. (Ive cleaned up the STG
though so its not `true` syntax)
* STG is very similar to Core but has one nice additional property:
* laziness is 'explicit'
* `case` = _evaluation_ and ONLY place evaluation occurs (true in
Core)
* `let` = _allocation_ and ONLY place allocation occurs (not true
in Core)
* So in STG we can explicitly see thunks being allocated for
laziness using `let`
* To view STG use:
~~~~
ghc -ddump-stg A.hs > A.stg
~~~~
# Strictness & Unboxing
* Consider the expression `x + y`, where x and y have type Int.
* In Haskell `x` & `y` must be represented by pointers to a
possibly unevaluated object
* Even if evaluated still represented by "boxed" values on the
heap
* So addition operation must unbox `x` & `y`, add them, and box
the result
* This can be a huge performance penalty in numeric heavy code if the
implementation is naive
* If we can we want to work with unboxed values as long and as much as
possible
* We can only do this though when we have determined that a value
`x` will always be evaluated (i.e is 'strict') to avoid breaking
the lazy semantics of Haskell
# Naive compilation of factorial
Consider this factorial implementation in Haskell:
~~~~ {.haskell}
fac :: Int -> Int -> Int
fac a 0 = a
fac a n = fac (n*a) (n-1)
~~~~
STG
~~~~ {.haskell}
fac = \ a n -> case n of
I# n# -> case n# of
0# -> a
_ -> let one = I# 1;
x = n - one
y = n * a;
in fac y x
~~~~
* We allocate thunks before the recursive call and box arguments
* But `fac` will immediately evaluate the thunks and unbox the values!
* With this strictness knowledge, the boxing and thunk creation are
unnecessary overhead
# GHC with strictness analysis and unboxing
If we compile in GHC with optimisations turned on:
~~~~ {.haskell}
one = I# 0#
-- worker :: Int# -> Int# -> Int#
$wfac = \ a# n# -> case n# of
0# -> a#
n'# -> case (n'# -# 1#) of
m# -> case (n'# *# a#) of
x# -> $wfac x# m#
-- wrapper :: Int -> Int -> Int
fac = \ a n -> case a of
I# a# -> case n of
I# n# -> case ($wfac a# n#) of
r# -> I# r#
~~~~
* Strictness analysis has discovered that `fac` is strict in both
arguments
* So creates a new 'worker' variant of `fac` that uses unboxed types
and no thunks
* Keeps original function `fac` though, referred to as the 'wrapper'
to supply the correct type interface for other code.
* As the wrapper uses unboxed types and is tail recursive, this will
compile to a tight loop in machine code!
# SpecConstr
The idea of the SpecConstr pass is to extend the strictness and
unboxing from before but to functions where arguments aren't strict in
every code path.
Consider this Haskell function:
~~~~ {.haskell}
drop :: Int -> [a] -> [a]
drop n [] = []
drop 0 xs = []
drop n (x:xs) = drop (n-1) xs
~~~~
* Would like to pass `n` unboxed but it isn't strict in the first
pattern
So we get this code in STG:
~~~~ {.haskell}
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> []
_ -> drop (I# (n# -# 1#)) xs
~~~~
* Notice how after the first time this function is called and we start
recursing, we could pass `n` unboxed
# SpecConstr
The SpecConstr pass takes advantage of this to create a specialised
version of `drop` that is only called after we have passed the first
check where we may not want to evaluate `n`.
Basically we aren't specialising the whole function but a particular
branch of it that is heavily used (ie. recursive)
~~~~ {.haskell}
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> []
_ -> drop' (n# -# 1#) xs
-- works with unboxed n
drop' n# xs = case xs of
[] -> []
(y:ys) -> case n# of
0# -> []
_ -> drop (n# -# 1#) xs
~~~~
* To stop the code size blowing up GHC limits the amount of
specialized functions it creates, specified with the
`-fspec-constr-threshol` and `-fspec-constr-count` flags
# Backend: _Core -> Assembly_
Final stage of GHC is compiling Core to an executable. The backend is
in two parts:
* STG -> Cmm: called the code generator in GHC
Cmm is a low level imperative language used in GHC. Basically a very
simple C like language. Just enough to abstract away hardware
registers, call conventions:
* Cmm exists to provide a common (easy) IR for the final backends to
work with.
* There are three _Cmm -> Object code_ backends in GHC: C code
generator using GCC, Native assembly code generator and an LLVM code
generator.
* C is for portability, NCG is for compilation speed, LLVM is for
'performance' and the future
# _STG -> Cmm_
So what has been handled and what is left to handle?
* By the STG stage we have:
* Simplified Haskell to a handful of constructs (variables,
literal, let, lambda, case and application)
* type classes, monads have all been dealt with
* laziness is nearly explicit through let constructs for
allocation and case for evaluation
* So we still have to deal with:
* Compiling these constructs efficiently, big focus will be
handling closures and garbage collection (lazy functional
languages involve a lot of allocation of short lived objects)
* Partial application (only remaining implicit allocation)
* Evaluating thunks and handling updates
# The STG Machine
The way the operational semantics of the STG language is defined is by
an abstract machine called 'The STG Machine'.
* The idea of an abstract machine is to give an operational semantics
to a language (STG in this case) that the source language (Haskell
in this case) can be 'easily' mapped to.
* But the abstract machine should also define an efficient way it
itself can be implemented on standard hardware.
* So basically its a virtual machine stepping stone. LLVM is a good
modern day example of this that is fairly widely known.
# _STG Machine -> Cmm_
Lets just look at some of the details of the code generator. The final
backends are all pretty straight forward (think simple C compiler).
The important parts of the code generator are:
* Closure representation
* Heap and Stack layout
* Call convention & partial application
* Graph reduction: thunks, update frames and black holes
* Case statements
* Pointer tagging and evaluation
* RTS and Garbage Collection
# Closure Representation
The STG machine represents function and data values as heap allocated
_closures_. Delayed computations, _thunks_, are also represented by
closure objects.
In GHC all Heap objects have the same layout:
| Closure | | | Info Table |
| 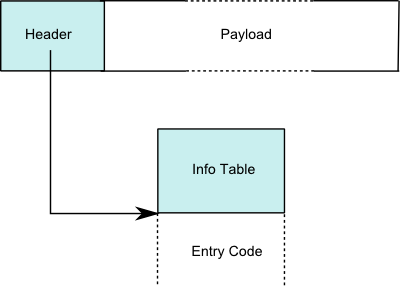 |
|
|
 |
* Header differs depending on closure type, all contain a pointer to
code though (even if it represents a value!)
* Payload contains the closures environment (e.g free variables,
function arguments)
* Layout describes the layout of payload for the garbage collector
* Notice how the pointer for the info table points to both the info
table and the code that will evaluate the closure
# Closure Representation
* Data Constructors:
~~~~ {.haskell}
data G = G (Int -> Int) {-# UNPACK #-} !Int
~~~~
* [Header | Pointers... | Non-pointers...]
* Payload is the values for the constructor
* Closure types of: CONSTR, CONSTR_p_n, CONSTR_STATIC
* Entry code for a constructor just returns
* Thunks:
~~~~ {.haskell}
range = between 1 10
f = \x -> let ys = take x range
in sum ys
~~~~
* [Header | Pointers... | Non-pointers...]
* Payload contains the free variables of the expression
* Differ from function closure in that they can be updated
* Clousre types of: THUNK, THUNK_p_n, THUNK_STATIC (`range` is a
static thunk, `ys` is a dynamic thunk)
* Entry code is the code for the expression
# Closure Representation
* Function Closures:
~~~~ {.haskell}
f = \x -> let g = \y -> x + y
in g x
~~~~
* [Header | Pointers... | Non-pointers...]
* Payload is the bound free variables (e.g in example above, g is
the function closure and x would be in its payload)
* Function types of: FUN, FUN_p_n, FUN_STATIC
* Entry code is the function code
* Partial Applications (PAP):
~~~~ {.haskell}
foldr (:)
~~~~
* [Header | Arity | Payload size | Function closure | Payload]
* Arity of the PAP (function of arity 3 with 1 argument applied
gives PAP of arity 2)
* Function closure is the function that has been partially applied
* PAPs should never be entered so the entry code is some failure
code
# Heap & Stack Layout
GHC has a very nice uniform way of managing the heap and stack.
* Heap:
* Heap at the lowest level is a linked list of blocks.
* All objects in the heap are represented by closure objects
* Even when for some of them the entry code doesn't make sense
* When entry code doesn't make sense, the code will either be
code that simply returns or code that throws and error
* Stack:
* The stack consists of a sequence of _frames_
* Each frame has the same layout as a heap object! So the stack
and the heap can often be treated uniformily
* Stacks until very recently were a single contiguous block of
memory. They are now a linked list of stack chunks.
* chunked stacks can be grown far easier but also are quicker to
traverse during GC since we can avoid entire chunks of the
stack if they haven't been touched since last GC.
* TSO (thread state object):
* Represents the complete state of a thread including it stack
* Are ordinary objects that live in the heap
* Important benefit of this approach is the GC can detect when
a blocked thread is unreachable and so will never be runnable
again
# Terminology 105
* _activation record_: An alternative name for a stack frame
* _forcing_: In the context of a thunk it means evaluating it
* _entering_: In the context of a closure it means evaluating it
* _node_: Node in the context of the entry code for a closure is a
pointer to the environment for the closure
# Call Convention
* GHC compiles code into a form called _Continuation Passing Style_:
* The idea here is that no function ever returns
* Instead a function returns by jumping to the closure at the top
of the stack
* Basically the code is always jumping from closure to closure so
before calling a function we simply setup the stack correctly to
have the control chain on it we want.
* Call convention is simple: first _n_ arguments in registers, rest on
the stack
* When entering a closure (a common case) the first argument is
always a pointer to the closures heap object (node) so it can access
its environment
* Return convention is also simple, return is made by jumping to the
entry code associated with the _info table_ of the topmost stack
frame OR in some cases we set the _R1_ register to point to the
return closure
~~~~ {.haskell}
id' x = x
~~~~
~~~~ {.c}
A_idzq_entry()
R1 = R2;
jump stg_ap_0_fast ();
~~~~
~~~~ {.c}
stg_ap_0_fast {
ENTER();
}
#define ENTER()
// ...
case
FUN,
// ...
PAP: { jump %ENTRY_CODE(Sp(0)); }
default: { info = %INFO_PTR(UNTAG(R1)); jump %ENTRY_CODE(info); }
~~~~
# Call Convention
Calling a known Haskell function:
Haskell
~~~~ {.haskell}
x :: Int -> Int
x z = (+) 2 (id z)
~~~~
Cmm
~~~~ {.c}
I64[Hp - 8] = spH_info; // create thunk on heap
I64[Hp + 0] = R2; // R2 = z, store argument in closure
R2 = stg_INTLIKE_closure+289; // first argument (static closure for '2')
R3 = Hp - 16; // second argument (closure pointer)
jump base_GHCziBase_plusInt (); // call (+) function
~~~~
# Call Convention
What happens though when we are calling an unknown function?
Haskell
~~~~ {.haskell}
unknown_app :: (Int -> Int) -> Int -> Int
unknown_app f x = f x
~~~~
Cmm
~~~~ {.c}
unknownzuapp_entry() {
cnO:
R1 = R2;
Sp = Sp + 4;
jump stg_ap_p_fast ();
}
~~~~
* Here we don't call the function directly as we don't statically known
the arity of the function.
* To deal with this, the STG machine has several pre-compiled functions
that handle 'generic application'
* Generic application has three cases to deal with:
* The functions arity and number of arguments match! So we simply
make a tail call to the functions entry code.
* The functions arity is greater than the number of supplied
argumnts. In this case we build a PAP closure and return that
closure to the continuation at the top of the stack
* The functions arity is less than the number of supplied
arguments. Here we push the number of arguments matching the
functions arity onto the stack, followed by a new continuation
that uses another generic apply function to deal with the
remaining arguments and the function that should be returned by
the first function.
# Data Constructors
Haskell
~~~~ {.haskell}
10
~~~~
Cmm
~~~~ {.c}
section "data" {
A_ten_closure:
const ghczmprim_GHCziTypes_Izh_static_info;
const 10;
}
~~~~
* Pointer to Constructor (`I#`)
* arguments to constructor (`10`)
# Pointer Tagging
* An optimization that GHC does is _pointer tagging_. The trick is to
use the final bits of a pointer which are usually zero (last 2 for
32bit, 3 on 64) for storing a 'tag'.
* GHC uses this tag for:
* If the object is a constructor, the tag contains the constructor
number (if it fits)
* If the object is a function, the tag contains the arity of the
function (if it fits)
* One optimization tag bit enable is that we can detect if a closure
has already been evaluated (by the presence of tag bits) and avoid
entering it
# Data Constructors
Haskell
~~~~ {.haskell}
build_just :: a -> Maybe a
build_just x = Just x
~~~~
Cmm
~~~~ {.c}
buildzujust_entry()
crp:
Hp = Hp + 16;
if (Hp > HpLim) goto crt; // Allocte heap space
I64[Hp - 8] = base_DataziMaybe_Just_con_info; // Just constructor tag
I64[Hp + 0] = R2; // store x in Just
R1 = Hp - 6; // setup R1 as argument to continuation
// (we do '- 6' and not '8' to set the pointer tag)
jump (I64[Sp + 0]) (); // jump to continuation
cru:
R1 = buildzujust_closure;
jump stg_gc_fun ();
crt:
HpAlloc = 16;
goto cru;
}
~~~~
# Case Statements
Haskell
~~~~ {.haskell}
mycase :: Maybe Int -> Int
mycase x = case x of Just z -> z; Nothing -> 10
~~~~
Cmm
~~~~ {.c}
mycase_entry() // corresponds to forcing 'x'
crG:
R1 = R2; // R1 = 'x'
I64[Sp - 8] = src_info; // setup case continuation
Sp = Sp - 8;
if (R1 & 7 != 0) goto crL; // check pointer tag to see if x eval'd
jump I64[R1] (); // x not eval'd, so eval
crL:
jump src_info (); // jump to case continuation
}
src_ret() // case continuation
crC:
v::I64 = R1 & 7; // get tag bits of 'x' and put in local variable 'v'
if (_crD::I64 >= 2) goto crE; // can use tag bits to check which constructor we have
R1 = stg_INTLIKE_closure+417; // 'Nothing' case
Sp = Sp + 8; // pop stack
jump (I64[Sp + 0]) (); // jump to continuation ~= return
crE:
R1 = I64[R1 + 6]; // get 'z' thunk inside Just
Sp = Sp + 8; // pop stack
R1 = R1 & (-8); // clear tags on 'z'
jump I64[R1] (); // force 'z' thunk
}
~~~~
# Graph Reduction: Thunks, Updates & Indirections
Lets take a look at the code for the `(x + 1)` thunk:
~~~~ {.haskell}
build_data :: Int -> Maybe Int
build_data x = Just (x + 1)
~~~~
Cmm
~~~~ {.c}
sus_entry()
cxa:
if (Sp - 24 < SpLim) goto cxc;
I64[Sp - 16] = stg_upd_frame_info; // setup update frame (closure type)
I64[Sp - 8] = R1; // set thunk to be updated (payload)
I64[Sp - 24] = sut_info; // setup continuation (+) continuation
Sp = Sp - 24; // increase stack
R1 = I64[R1 + 16]; // grab 'x' from environment
if (R1 & 7 != 0) goto cxd; // check if 'x' is eval'd
jump I64[R1] (); // not eval'd so eval
cxc: jump stg_gc_enter_1 ();
cxd: jump sut_info (); // 'x' eval'd so jump to (+) continuation
}
sut_ret()
cx0:
Hp = Hp + 16;
if (Hp > HpLim) goto cx5;
v::I64 = I64[R1 + 7] + 1; // perform ('x' + 1)
I64[Hp - 8] = ghczmprim_GHCziTypes_Izh_con_info; // setup Int closure
I64[Hp + 0] = v::I64; // setup Int closure
R1 = Hp - 7; // point R1 to computed thunk value (with tag)
Sp = Sp + 8; // pop stack
jump (I64[Sp + 0]) (); // jump to continuation ('stg_upd_frame_info')
cx6: jump stg_gc_enter_1 ();
cx5:
HpAlloc = 16;
goto cx6;
}
~~~~
# Graph Reduction: Thunks & Updates
* The interesting thing here is that once the thunk is forced and
computes `(x + 1)` it doesn't return to the continuation at the top
of the stack
~~~~ {.c}
I64[Sp - 16] = stg_upd_frame_info; // setup update frame (closure type)
I64[Sp - 8] = R1; // set thunk to be updated (payload)
~~~~
* Instead it returns to the `stg_upd_frame_info` function
* This function is reponsible for taking the thunks computed value and
replacing the thunk with this computed value to avoid it being
recomputed
* The replacing is done by changing the entry code for the thunk to be
an 'indirection' which is simply code that returns a pointer to
another closure.
* The GC will remove indirections during copying, changing code that
pointed to a indirection (evaluated thunk) to the actual value
closure.
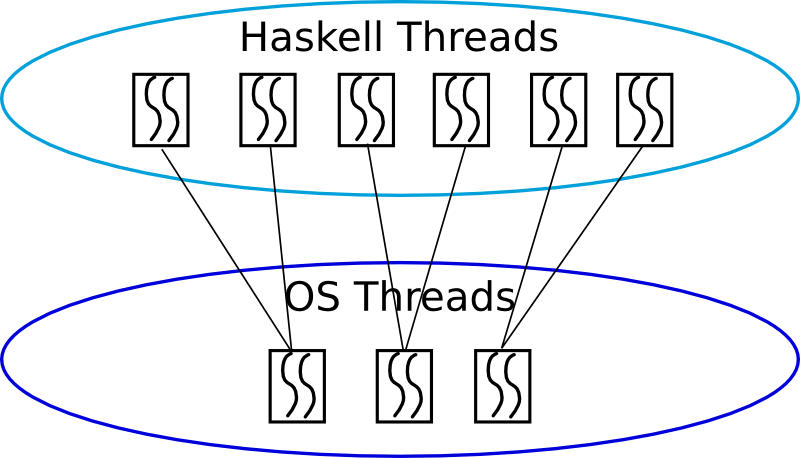
# RTS & Garbage Collection
* GHC has a n:m threading model:
* n Haskell light weight threads running on m OS threads (thread pool model)
* context switches can occur when garbage collection checks are invoked
based on typical time slice model with round robbin scheduling
* the frequency of this gives close to a pre-emptive thread model
# RTS & Garbage Collection
* GC uses a [generational copy collector design](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Rts/Storage/GC)
* Basic idea of a generational collector is to divide objects up
into generations (time they've been alive) since young objects
have a higher probability of becoming garbage. We can now just
GC one generation at a time in an incremental fashion to speed
up GC.
* Basic idea of a copy collectors is you have two heaps, one is
the current heap and during GC you start with a list of known
live objects
(["roots"](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Rts/Storage/GC/Roots)),
recurisvely trace their dependencies (finding live objects) and
copy all found objects to the other heap. Anything not copied
isn't referenced by anything so is dead. Now switch heaps.

# RTS & Garbage Collection
* [Block Allocator](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Rts/Storage/BlockAlloc)
is at the base of the GC:
* Uses a linked list of blocks where within a block we allocate
using a simple bump pointer (heap and stack mangaged this way)
* Bump pointer is where we simply have a current block to allocate with
a pointer to the next free space to allocate in. To allocate we check
there is enough space left in the block and if so bump the pointer
* Block size is chosen such that it's rare we need to allocate an
object larger than a block
~~~~ {.c}
AMod_abc_entry:
entry:
_v = R2 // collect arguments
_w = R3
if (Sp - 40 < SpLim) goto spL // check enough stack free
Hp = Hp + 20 // allocate heap space
if (Hp > HpLim) goto hpL // check allocation is ok
[... funtion code now we have stack and heap space needed ...]
Sp = Sp - 32 // bump stack pointer to next free word
jump ... // jump to next continuation
hpL:
HpAlloc = 20 // inform how much hp space we need
spL:
R1 = AMod_abc_closure; // set return point
jump stg_gc_fun // call GC
~~~~
* Above is the _Cmm_ code typically generated for functions that
need to allocate. Notice we simply bump the `Hp` and `Sp`
registers for allocation after we check there is enough space.
* We don't need to tell the GC how much stack to allocate as it
just allocates the stack in fixed block sizes
# Bringing it all home
No lecture on Compilers is complete without assembly code!
~~~~ {.haskell}
add :: Int -> Int -> Int
add x y = x + y + 2
~~~~
~~~~ {.assembly}
A_add_info:
.LcvZ:
leaq -16(%rbp),%rax
cmpq %r15,%rax
jb .Lcw1
movq %rsi,-8(%rbp)
movq %r14,%rbx
movq $sul_info,-16(%rbp)
addq $-16,%rbp
testq $7,%rbx
jne sul_info
jmp *(%rbx)
.Lcw1:
movl $A_add_closure,%ebx
jmp *-8(%r13)
sul_info:
.LcvS:
movq 8(%rbp),%rax
movq 7(%rbx),%rcx
movq %rcx,8(%rbp)
movq %rax,%rbx
movq $suk_info,0(%rbp)
testq $7,%rbx
jne suk_info
jmp *(%rbx)
suk_info:
.LcvK:
addq $16,%r12
cmpq 144(%r13),%r12
ja .LcvP
movq 7(%rbx),%rax
addq $2,%rax
movq 8(%rbp),%rcx
addq %rax,%rcx
movq $ghczmprim_GHCziTypes_Izh_con_info,-8(%r12)
movq %rcx,0(%r12)
leaq -7(%r12),%rbx
addq $16,%rbp
jmp *0(%rbp)
.LcvP:
movq $16,184(%r13)
.LcvQ:
jmp *-16(%r13)
~~~~
# Finished!
* So that's is all I can cover in this lecture.
* I haven't covered a few significant areas:
* Typechecking
* The scheduler: threads, multi-processor support
* Foreign Function Interface
* Profiling
* Infrastructure of the compiler: Interface files, packages,
modular compilation... ect
* Final code generators
* GHCi
* The finer details of lazy evaluation: sharing, update frames,
blackholes
# Resources & References
Here are some resources to learn about GHC, they were also used to
create these slides:
* GHC Wiki: [Developer Documentation](http://hackage.haskell.org/trac/ghc/wiki/Commentary)
* GHC Wiki: [I know kung fu: learning STG by example](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Compiler/GeneratedCode)
* Wikipedia: [System F](http://en.wikipedia.org/wiki/System_F)
* Paper: [Multi-paradigm Just-In-Time Compilation](http://www.cse.unsw.edu.au/~pls/thesis/dons-thesis.ps.gz)
* Paper: [Implementing lazy functional languages on stock hardware: the Spineless Tagless G-machine](http://research.microsoft.com/en-us/um/people/simonpj/papers/spineless-tagless-gmachine.ps.gz#26pub=34)
* Paper: [Implementing Functional Languages: a tutorial](http://research.microsoft.com/en-us/um/people/simonpj/papers/pj-lester-book/)
* Paper: [Runtime support for Multicore Haskell](http://research.microsoft.com/apps/pubs/default.aspx?id=79856)
* Paper: [Multicore Garbage Collection with Local Heaps](http://www.google.com/url?sa=t&rct=j&q=Multicore%2BGarbage%2BCollection%2Bwith%2BLocal%2BHeaps&source=web&cd=1&ved=0CCAQFjAA&url=http%3A%2F%2Fcommunity.haskell.org%2F~simonmar%2Fpapers%2Flocal-gc.pdf&ei=YmXBTq3hLoatiAKq3tT5Ag&usg=AFQjCNGH0SgCfqpKQkQxq11Azl3btSk5Dw&sig2=OVzFyZrZRopkhlo7yriv_w)
* Paper: [Parallel generational-copying garbage collection with a block-structured heap](http://research.microsoft.com/en-us/um/people/simonpj/papers/parallel-gc/index.htm)
* Paper: [Making a fast curry: Push/enter vs eval/apply for higher-order languages](http://research.microsoft.com/en-us/um/people/simonpj/papers/eval-apply/)
* Paper: [An External Representation for the GHC Core Language](http://www.haskell.org/ghc/docs/6.10.4/html/ext-core/core.pdf)
* Paper: [A transformation-based optimiser for Haskell](http://research.microsoft.com/~simonpj/Papers/comp-by-trans-scp.ps.gz)
* Paper: [Playing by the rules: rewriting as a practical optimisation technique in GHC](http://research.microsoft.com/~simonpj/Papers/rules.htm)
* Paper: [Secrets of the Inliner](http://www.research.microsoft.com/~simonpj/Papers/inlining/index.htm)
* Paper: [Unboxed Values as First-Class Citizens](http://www.haskell.org/ghc/docs/papers/unboxed-values.ps.gz)