% A Haskell Compiler
% David Terei
# Why understand how GHC works?
* Understand Core & STG -- performance.
* Familiarity with functional terminology.
* Understand execution model -- reasonable cost model.
# The pipeline of GHC
Haskell -> GHC Haskell -> Core -> STG -> Cmm -> Assembly
# GHC supports Haskell on top of an unsafe variant
Primitive types (GHC.Prim):
* Char#, Int#, Word#, Double#, Float#
* Array#, ByteArray#, ArrayArray#,
* MutVar#, TVar#, MVar#
* State#, exceptions
All primitive types are _unlifted_ -- can't contain $\bot$.
# GHC supports Haskell on top of an unsafe variant
All variants of Int (In8, Int16, Int32, Int64) are represented
internally by Int# (64bit) on a 64bit machine.
``` {.haskell}
data Int32 = I32# Int# deriving (Eq, Ord, Typeable)
instance Num Int32 where
(I32# x#) + (I32# y#) = I32# (narrow32Int# (x# +# y#))
...
```
Data constructors _lift_ a type, allowing $\bot$.
# GHC implements IO through the RealWorld token
* IO Monad is a state passing monad.
``` {.haskell}
newtype IO a = IO (State# RealWorld -> (# State# RealWorld, a #))
returnIO :: a -> IO a
returnIO x = IO $ \ s -> (# s, x #)
bindIO :: IO a -> (a -> IO b) -> IO b
bindIO (IO m) k = IO $ \ s -> case m s of (# new_s, a #) -> unIO (k a) new_s
```
* `RealWorld` token enforces ordering through data dependence.
``` {.haskell}
unsafePerformIO :: IO a -> a
unsafePerformIO m = unsafeDupablePerformIO (noDuplicate >> m)
unsafeDupablePerformIO :: IO a -> a
unsafeDupablePerformIO (IO m) = lazy (case m realWorld# of (# _, r #) -> r)
```
* Various unsafe functions throw away `RealWorld` token.
# Core: a small function intermediate language
* Idea: map Haskell to a small lanuage for easier optimization and
compilation.
* Functional lazy language
* It consists of only a hand full of constructs!
```
variables, literals, let, case, lambda abstraction, application
```
* In general think, `let` means allocation, `case` means evaluation.
# Core in one slide
``` {.haskell}
data Expr b -- "b" for the type of binders,
= Var Id
| Lit Literal
| App (Expr b) (Arg b)
| Lam b (Expr b)
| Let (Bind b) (Expr b)
| Case (Expr b) b Type [Alt b]
| Type Type
| Cast (Expr b) Coercion
| Coercion Coercion
| Tick (Tickish Id) (Expr b)
data Bind b = NonRec b (Expr b)
| Rec [(b, (Expr b))]
type Arg b = Expr b
type Alt b = (AltCon, [b], Expr b)
data AltCon = DataAlt DataCon | LitAlt Literal | DEFAULT
```
Lets now look at how Haskell is compiled to
[Core](http://hackage.haskell.org/trac/ghc/wiki/Commentary/Compiler/CoreSynType).
# GHC Haskell to Core: monomorphic functions
Haskell
``` {.haskell}
idChar :: Char -> Char
idChar c = c
```
Core
``` {.haskell}
idChar :: GHC.Types.Char -> GHC.Types.Char
[GblId, Arity=1, Caf=NoCafRefs]
idChar = \ (c :: GHC.Types.Char) -> c
```
# GHC Haskell to Core: polymorphic functions
Haskell
``` {.haskell}
id :: a -> a
id x = x
idChar2 :: Char -> Char
idChar2 = id
```
Core
``` {.haskell}
id :: forall a. a -> a
id = \ (@ a) (x :: a) -> x
idChar2 :: GHC.Types.Char -> GHC.Types.Char
idChar2 = id @ GHC.Types.Char
```
# GHC Haskell to Core: polymorphic functions
Haskell
``` {.haskell}
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
```
Core
``` {.haskell}
map :: forall a b. (a -> b) -> [a] -> [b]
map = \ (@ a) (@ b) (f :: a -> b) (xs :: [a]) ->
case xs of _ {
[] -> GHC.Types.[] @ b;
: y ys -> GHC.Types.: @ b (f y) (map @ a @ b f ys)
}
```
New case syntax to make obvious that evaluation is happening:
``` {.haskell}
case e of result {
__DEFAULT -> result
}
```
# Where transformed to let
Haskell
``` {.haskell}
dox :: Int -> Int
dox n = x * x
where x = n + 2
```
Core
``` {.haskell}
dox :: GHC.Types.Int -> GHC.Types.Int
dox = \ (n :: GHC.Types.Int) ->
let {
x :: GHC.Types.Int
x = GHC.base.plusInt n (GHC.Types.I# 2)
}
in GHC.base.multInt x x
```
# Patterns matching transformed to case statements
Haskell
``` {.haskell}
iff :: Bool -> a -> a -> a
iff True x _ = x
iff False _ y = y
```
Core
``` {.haskell}
iff :: forall a. GHC.Bool.Bool -> a -> a -> a
iff = \ (@ a) (d :: GHC.Bool.Bool) (x :: a) (y :: a) ->
case d of _
GHC.Bool.False -> y
GHC.Bool.True -> x
```
# Type classes transformed to dictionaries
Haskell
``` {.haskell}
typeclass MyEnum a where
toId :: a -> Int
fromId :: Int -> a
```
Core
``` {.haskell}
data MyEnum a = DMyEnum (a -> Int) (Int -> a)
toId :: forall a. MyEnum a => a -> GHC.Types.Int
toId = \ (@ a) (d :: MyEnum a) (x :: a) ->
case d of _
DMyEnum f1 _ -> f1 x
fromId :: forall a. MyEnum a => GHC.Types.Int -> a
fromId = \ (@ a) (d :: MyEnum a) (x :: a) ->
case d of _
DMyEnum _ f2 -> f2 x
```
# A dictionary constructed for each instance
Haskell
``` {.haskell}
instance MyEnum Int where
toId = id
fromId = id
```
Core
``` {.haskell}
fMyEnumInt :: MyEnum GHC.Types.Int
fMyEnumInt =
DMyEnum @ GHC.Types.Int
(id @ GHC.Types.Int)
(id @ GHC.Types.Int)
```
# Dictionaries constructed from dictionaries
Haskell
``` {.haskell}
instance (MyEnum a) => MyEnum (Maybe a) where
toId (Nothing) = 0
toId (Just n) = toId n
fromId 0 = Nothing
fromId n = Just $ fromId n
```
Core
``` {.haskell}
fMyEnumMaybe :: forall a. MyEnum a => MyEnum (Maybe a)
fMyEnumMaybe = \ (@ a) (dict :: MyEnum a) ->
DMyEnum @ (Maybe a)
(fMyEnumMaybe_ctoId @ a dict)
(fMyEnumMaybe_cfromId @ a dict)
fMyEnumMaybe_ctoId :: forall a. MyEnum a => Maybe a -> Int
fMyEnumMaybe_ctoId = \ (@ a) (dict :: MyEnum a) (mx :: Maybe a) ->
case mx of _
Nothing -> I# 0
Just n -> case (toId @ a dict n) of _
I# y -> I# (1 +# y)
```
# UNPACK unboxes types
Haskell
``` {.haskell}
data Point = Point {-# UNPACK #-} !Int
{-# UNPACK #-} !Int
```
Core
``` {.haskell}
data Point = Point Int# Int#
```
* Only one data type for Point exists, GHC doesn't duplicate it.
# UNPACK not always a good idea
Haskell
``` {.haskell}
addP :: P -> Int
addP (P x y ) = x + y
```
Core
``` {.haskell}
addP :: P -> Int
addP = \ (p :: P) ->
case p of _ {
P x y -> case +# x y of z {
__DEFAULT -> I# z
}
}
```
* Great code here as working with unboxed types.
# UNPACK not always a good idea
Haskell
``` {.haskell}
module M where
{-# NOINLINE add #-}
add x y = x + y
module P where
addP_bad (P x y) = add x y
```
Core
``` {.haskell}
addP_bad = \ (p :: P) ->
case p of _ {
P x y ->
let { x' = I# x
y' = I# y
} in M.add x' y'
}
```
* Need to unfortunately rebox the types.
# Core Summary
* Look at Core to get an idea of how your code will perform.
* Can see boxing an unboxing.
* Language still lazy but `case` means evaluation.
# Middle of GHC: _Core -> Core_
A lot of the optimizations that GHC does is through core to core
transformations.
Lets look at two of them:
* Strictness and unboxing
* SpecConstr
```
Fun Fact: Estimated that functional languages gain 20 - 40%
improvement from inlining Vs. imperative languages which gain 10 - 15%
```
# Strictness & Unboxing
Consider this factorial implementation in Haskell:
``` {.haskell}
fac :: Int -> Int -> Int
fac x 0 = a
fac x n = fac (n*x) (n-1)
```
* In Haskell `x` & `n` must be represented by pointers to a possibly
unevaluated objects (thunks)
* Even if evaluated still represented by "boxed" values on the heap
# Strictness & Unboxing
Core
``` {.haskell}
fac :: Int -> Int -> Int
fac = \ (x :: Int) (n :: Int) ->
case n of _ {
I# n# -> case n# of _
0# -> x
__DEFAULT -> let { one = I# 1
n' = n - one
x' = n * x
}
in fac x' n'
```
* We allocate thunks before the recursive call and box arguments
* But `fac` will immediately evaluate the thunks and unbox the values!
# GHC with strictness analysis
Compile `fac` with optimizations.
``` {.haskell}
wfac :: Int# -> Int# -> Int#
wfac = \ x# n# ->
case n# of _
0# -> x#
_ -> case (n# -# 1#) of n'#
_ -> case (n# *# x#) of x'#
_ -> $wfac x'# n'#
fac :: Int -> Int -> Int
fac = \ a n ->
case a of
I# a# -> case n of
I# n# -> case ($wfac a# n#) of
r# -> I# r#
```
* Create an optimized 'worker' and keep original function as 'wrapper'
to preserve interface.
* Must preserve semantics of $\bot$ --
`fac` $\bot$ `n = optimized(fac)` $\bot$ `n`
# SpecConstr: Extending strictness analysis to paths
The idea of the SpecConstr pass is to extend the strictness and
unboxing from before but to functions where arguments aren't strict in
every code path.
Consider this Haskell function:
``` {.haskell}
drop :: Int -> [a] -> [a]
drop n [] = []
drop 0 xs = xs
drop n (x:xs) = drop (n-1) xs
```
* Not strict in first argument:
* `drop` $\bot$ [] = []
* `drop` $\bot$ (x:xs) = $\bot$
# SpecConstr: Extending strictness analysis to paths
So we get this code without extra optimization:
``` {.haskell}
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> []
_ -> let n' = I# (n# -# 1#)
in drop n' ys
```
* But after the first time we call drop, we are strict in `n` and
always evaluate it!
# SpecConstr
The SpecConstr pass takes advantage of this to create a specialised
version of `drop` that is only called after we have passed the first
check.
``` {.haskell}
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> []
_ -> drop' (n# -# 1#) xs
-- works with unboxed n
drop' n# xs = case xs of
[] -> []
(y:ys) -> case n# of
0# -> []
_ -> drop (n# -# 1#) xs
```
* To stop code size blowing up, GHC limits the amount of specialized
functions it creates (specified with the `-fspec-constr-threshol`
and `-fspec-constr-count` flags).
# STG Code
* After Core, GHC compiles to another intermediate language called
STG.
* STG is very similar to Core but has one nice additional property:
* laziness is 'explicit'
* `case` = _evaluation_ and ONLY place evaluation occurs (true in
Core)
* `let` = _allocation_ and ONLY place allocation occurs (not true
in Core)
* So in STG we can explicitly see thunks being allocated for
laziness using `let`
* To view STG use:
~~~~
ghc -ddump-stg A.hs > A.stg
~~~~
# STG Code
Haskell
``` {.haskell}
map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (x:xs) = f x : map f xs
```
STG
``` {.haskell}
map :: forall a b. (a -> b) -> [a] -> [b]
map = \r [f xs]
case xs of _
[] -> [] []
: z zs -> let { bds = \u [] map f zs;
bd = \u [] f z; }
in : [bd bds]
```
* Lambda abstraction as `[arg1 arg2] f`
* `\r` - re-entrant
* `\u` - updatable (i.e., thunk)
# Graph Reduction as a computational model for Haskell
Graph reduction is a good computational model for lazy functional languages.
~~~~ {.haskell}
f g = let x = 2 + 2
in (g x, x)
~~~~
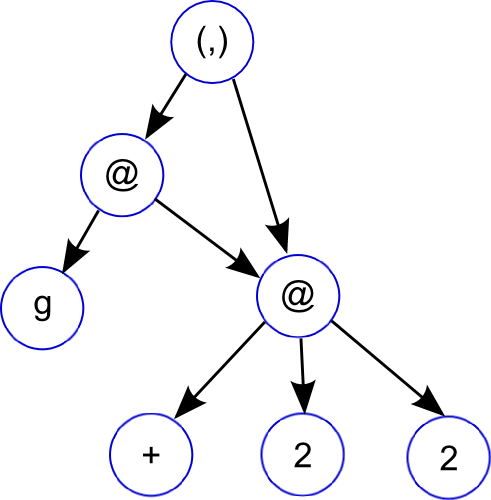
# Graph Reduction as a computational model for Haskell
Graph reduction is a good computational model for lazy functional languages.
~~~~ {.haskell}
f g = let x = 2 + 2
in (g x, x)
~~~~
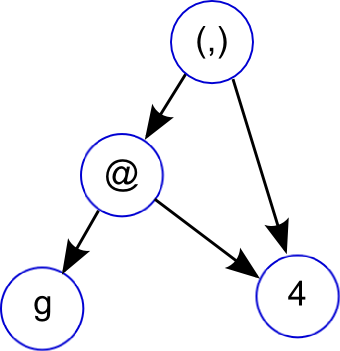
# Graph Reduction as a computational model for Haskell
Graph reduction is a good computational model for lazy functional languages.
* Graph reduction allows lazy evaluation and sharing
* _let_: adds new node to graph.
* _case_: expression evaluation, causes the graph to be reduced.
* When a node is reduced, it is replaced (or _updated_) with its result
Can think of your Haskell program as progressing by either adding new nodes to
the graph or reducing existing ones.
# GHC execution model
* GHC uses closures as a unifying representation.
* All objects in the heap are closures.
* A stack frame is a closure.
* GHC uses continuation-passing-style.
* Always jump to top stack frame to return.
* Functions will prepare stack in advance to setup call chains.
# Closure Representation
| Closure | | | Info Table |
| 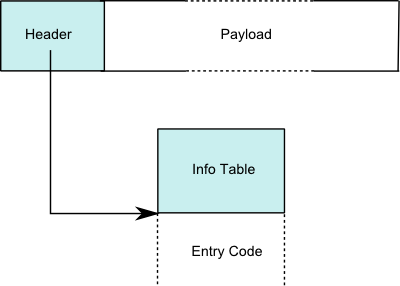 |
|
|
 |
* Header usually just a pointer to the code and metadata for the closure.
* Get away with single pointer through positive and negative offsets.
* Payload contains the closures environment (e.g free variables,
function arguments)
# Data closure
``` {.haskell}
data G = G (Int -> Int) {-# UNPACK #-} !Int
```
* `[Header | Pointers... | Non-pointers...]`
* Payload is the values for the constructor
* Entry code for a constructor just returns
``` {.asm}
jmp Sp[0]
```
# Function closures
``` {.haskell}
f = \x -> let g = \y -> x + y
in g x
```
* [Header | Pointers... | Non-pointers...]
* Payload is the bound free variables, e.g.,
* `[ &g | x ]`
* Entry code is the function code
# Partial application closures (PAP)
``` {.haskell}
foldr (:)
```
* `[Header | Arity | Payload size | Function | Payload]`
* Arity of the PAP (function of arity 3 with 1 argument applied
gives PAP of arity 2)
* Function is the closure of the function that has been partially applied
# Thunk closures
``` {.haskell}
range = [1..100]
```
* `[Header | Pointers... | Non-pointers...]`
* Payload contains the free variables of the expression
* Differ from function closure in that they can be updated
* Entry code is the code for the expression
# Calling convention
* On X86 32bit - all arguments passed on stack
* On X86 64bit - first 5 arguments passed in registers, rest on stack
* `R1` register in Cmm code usually is a pointer to the current closure (i.e.,
similar to `this` in OO languages).
# Handling thunk updates
* Thunks once evaluated should update their node in the graph to be the
computed value.
* GHC uses a _self-updating-model_ -- code unconditionally jumps to a thunk. Up
to thunk to update itself, replacing code with value.

# Handling thunk updates
``` {.haskell}
mk :: Int -> Int
mk x = x + 1
```
``` {.c}
// thunk entry - setup stack, evaluate x
mk_entry()
entry:
if (Sp - 24 < SpLim) goto gc;
I64[Sp - 16] = stg_upd_frame_info; // setup update frame (closure type)
I64[Sp - 8] = R1; // set thunk to be updated (payload)
I64[Sp - 24] = mk_exit; // setup continuation (+) continuation
Sp = Sp - 24; // increase stack
R1 = I64[R1 + 8]; // grab 'x' from environment
jump I64[R1] (); // eval 'x'
gc: jump stg_gc_enter_1 ();
}
```
# Handling thunk updates
``` {.haskell}
mk :: Int -> Int
mk x = x + 1
```
``` {.c}
// thunk exit - setup value on heap, tear-down stack
mk_exit()
entry:
Hp = Hp + 16;
if (Hp > HpLim) goto gc;
v::I64 = I64[R1] + 1; // perform ('x' + 1)
I64[Hp - 8] = GHC_Types_I_con_info; // setup Int closure
I64[Hp + 0] = v::I64;
R1 = Hp; // point R1 to computed thunk value
Sp = Sp + 8; // pop stack
jump (I64[Sp + 0]) (); // jump to continuation ('stg_upd_frame_info')
gc: HpAlloc = 16;
jump stg_gc_enter_1 ();
}
```
# stg_upd_frame_info code updates a thunk with its value
* To update a thunk with its value we need to change its header pointer.
* Should point to code that simply returns now.
* Payload also now needs to include the value.
* Naive solution would be to synchronize on every thunk access.
* But we don't need to! Races on thunks are fine since we can rely on purity.
Races just leads to duplication of work.
# stg_upd_frame_info code updates a thunk with its value
Thunk closure:
* `[Header | Payload]`
* `Header` = `[ Info Table Pointer | Result Slot ]`
* Result slot empty when thunk unevaluated.
* Update code, first places result in result slot and secondly changes the info
table pointer.
* Safe to do without synchronization (need write barrier) on all architectures
GHC supports.
# Avoiding entering values
* Evaluation model is we always enter a closure, even values.
* This is poor for performance, we prefer to avoid entering values every single
time.
* An optimization that GHC does is _pointer tagging_. The trick is to
use the final bits of a pointer which are usually zero (last 2 for
32bit, 3 on 64) for storing a 'tag'.
* GHC uses this tag for:
* If the object is a constructor, the tag contains the constructor
number (if it fits)
* If the object is a function, the tag contains the arity of the
function (if it fits)
# Avoiding entering values
Our example code from before:
``` {.haskell}
mk :: Int -> Int
mk x = x + 1
```
Changes with pointer tagging:
``` {.c}
mk_entry()
entry:
...
R1 = I64[R1 + 16]; // grab 'x' from environment
if (R1 & 7 != 0) goto cxd; // check if 'x' is eval'd
jump I64[R1] (); // not eval'd so eval
cxd: jump mk_exit (); // 'x' eval'd so jump to (+) continuation
}
mk_exit()
cx0:
I64[Hp - 8] = ghczmprim_GHCziTypes_Izh_con_info; // setup Int closure
I64[Hp + 0] = v::I64; // setup Int closure
R1 = Hp - 7; // point R1 to computed thunk value (with tag)
...
}
```
# Pointer tagging makes your own data types efficient
* If the closure is a constructor, the tag contains the constructor number (if
it fits).
``` {.haskell}
data MyBool a = MTrue a | MFalse a
```
* Will be as efficient as using an `Int#` for representing true and false.